Thermodynamics Work

Work from Friday (04/12/24)

Entropy

• Energy naturally wants to spread out
• Entropy (S) is a measure of how spread out (evenly distributed) energy is (“energy dilution”)
• Entropy commonly has units of J mol^–1 K–1

Energy is more spread out in the object on the right (below) than on the left.

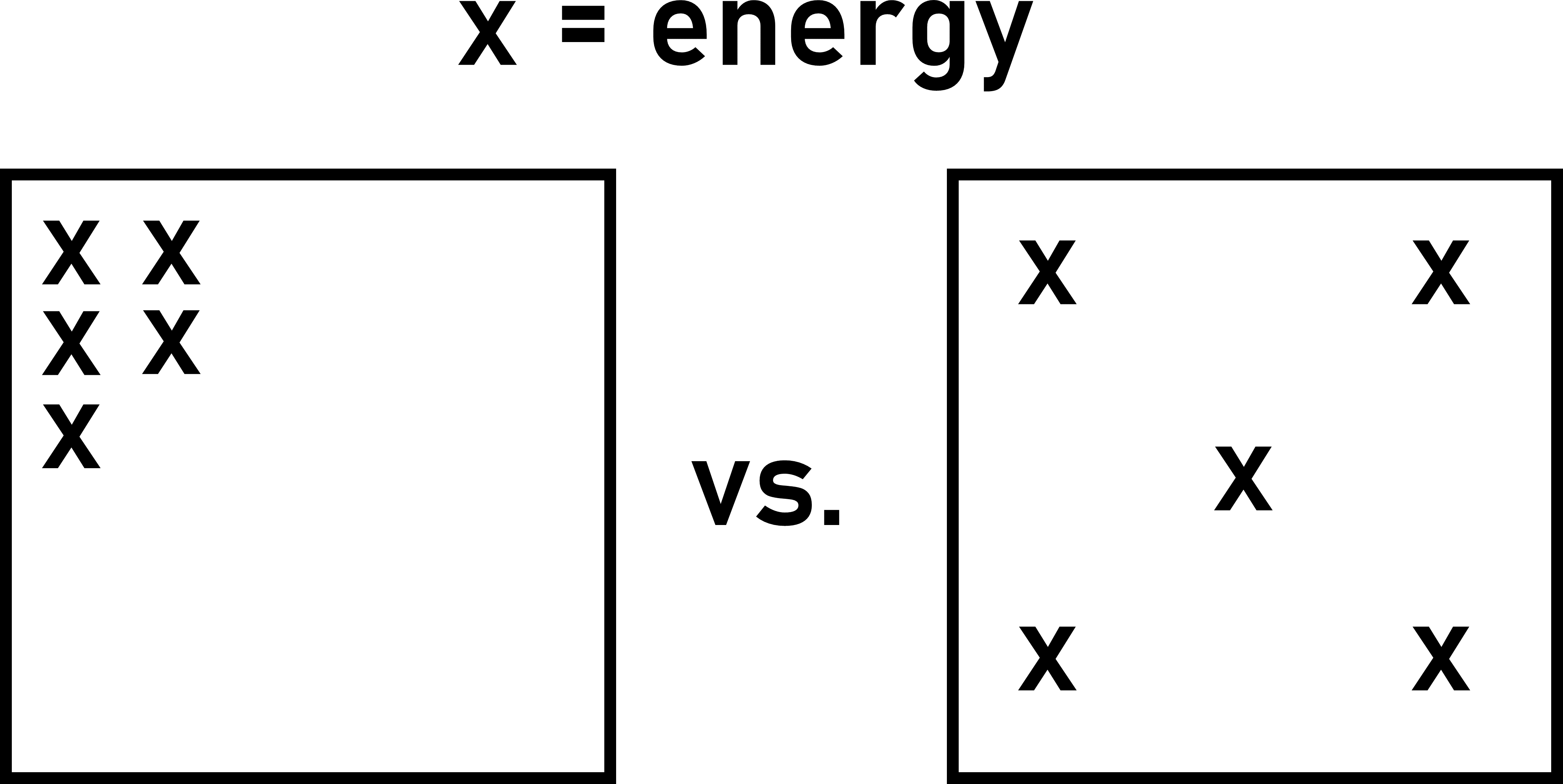
Example – Entropy change of two objects of differing temperature

Consider two objects of different temperature. Each object has a some non-zero amount of entropy. The colder object has less entropy than the hotter object.

Consider moving 10 kJ worth of energy into each object.

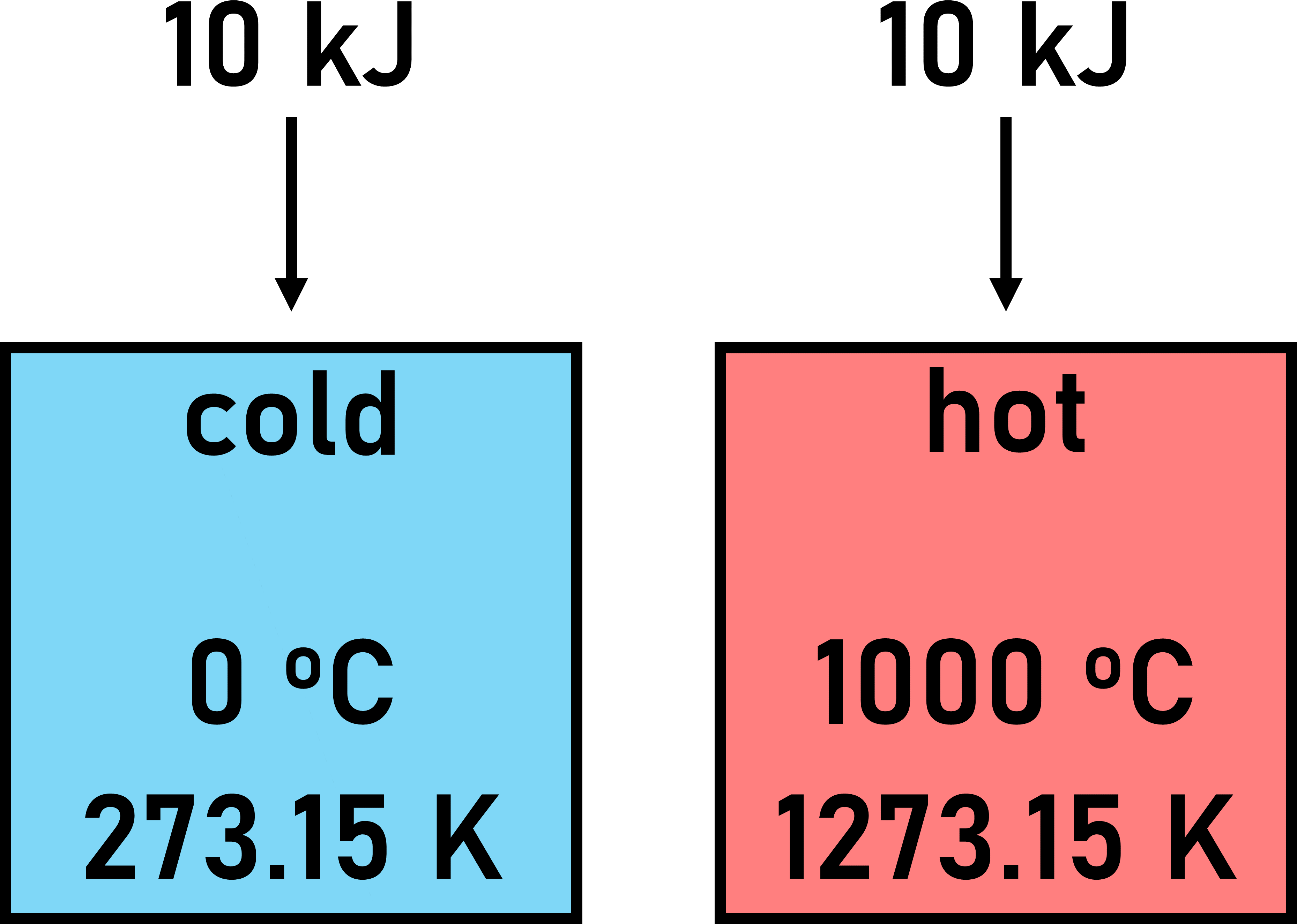
We can find the change in entropy (ΔS) of each object when this process occurs.

Cold Object

Recognize that the enthalpy change (ΔH) of the cold object is +10 kJ. The temperature (T) of the cold object is 273.15 K.

\[\begin{align*} \Delta S_{\mathrm{cold}} &= \dfrac{\Delta H}{T}\\[1.5ex] &= \dfrac{10~\mathrm{kJ}}{273.15~\mathrm{K}} \\[1.5ex] &= 36.6~\mathrm{J~K^{-1}} \end{align*}\]

Hot Object

Recognize that the enthalpy change (ΔH) of the hot object is +10 kJ. The temperature (T) of the hot object is 1273.15 K.

\[\begin{align*} \Delta S_{\mathrm{hot}} &= \dfrac{\Delta H}{T}\\[1.5ex] &= \dfrac{10~\mathrm{kJ}}{1273.15~\mathrm{K}} \\[1.5ex] &= 7.9~\mathrm{J~K^{-1}} \end{align*}\]

The cold object experienced a greater entropy change than the hot object. Energy was more evenly distributed in an object that started at a colder temperature and less entropy.

Example – Heat flows from hot to cold spontaneously

If the surroundings around these objects was at 25 °C, the cold object would absorb energy from the surroundings since the cold object is colder than the surroundings. The hot object would not absorb energy from the surroundings since the hot object is hotter than the surroundings.

The following entropy equation of the universe

\[\Delta S_{\mathrm{universe}} = \Delta S_{\mathrm{surroundings}} + \Delta S_{\mathrm{system}}\]

can be used to verify these outcomes. For any spontaneous process, ΔS_universe is positive.

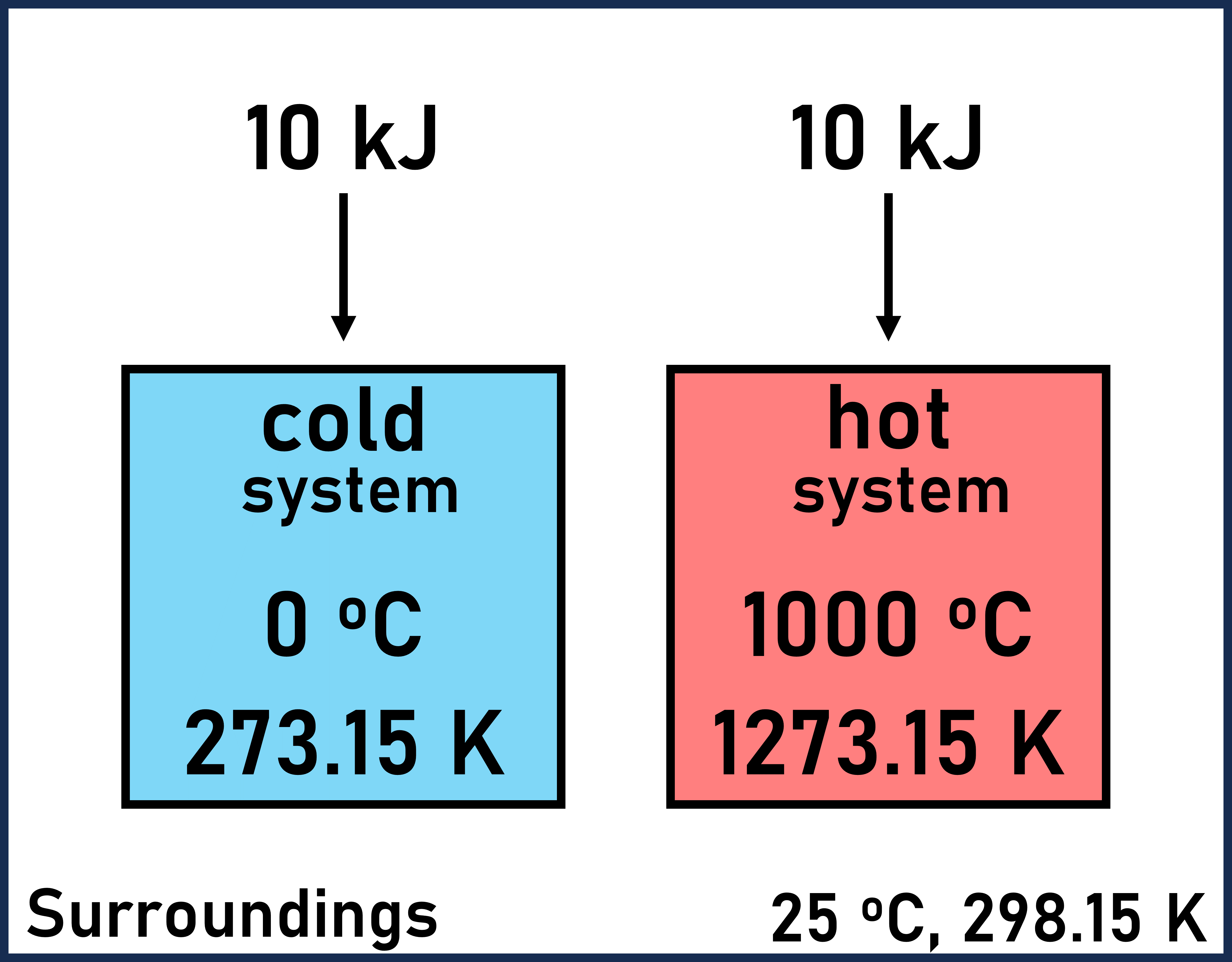
Cold Object

We know that the cold object will absorb energy from the warmer surroundings. Therefore, ΔS_universe should be positive for this process.

Determine the entropy change for the surroundings. We know that the enthalpy change (ΔH) for the surroundings should be –10 kJ since the surroundings is losing that much energy. The temperature (T) of the surroundings is 298.15 K.

\[\begin{align*} \Delta S_{\mathrm{surroundings}} &= \dfrac{\Delta H}{T} \\[1.5ex] &= \dfrac{-10~\mathrm{kJ}}{298.15~\mathrm{K}} \left ( \dfrac{10^3~\mathrm{J}}{\mathrm{kJ}} \right ) \\[1.5ex] &= -33.6~\mathrm{J~K^{-1}} \end{align*}\]

Now determine the entropy change of the universe for this process.

\[\begin{align*} \Delta S_{\mathrm{universe}} &= \Delta S_{\mathrm{surroundings}} + \Delta S_{\mathrm{system}} \\[1.5ex] &= -33.6~\mathrm{J~K^{-1}} + 36.6~\mathrm{J~K^{-1}} \\[1.5ex] &= 3~\mathrm{J~K^{-1}} \end{align*}\]

The change in entropy of the universe is positive so the process is spontaneous.

Hot Object

We can determine the change in entropy of the universe for the process of the hot object absorbing 10 kJ worth of heat from the colder surroundings. Use the previously calculated ΔS_hot and ΔS_surroundings.

\[\begin{align*} \Delta S_{\mathrm{universe}} &= \Delta S_{\mathrm{surroundings}} + \Delta S_{\mathrm{system}} \\[1.5ex] &= -33.6~\mathrm{J~K^{-1}} + 7.9~\mathrm{J~K^{-1}} \\[1.5ex] &= -25.7~\mathrm{J~K^{-1}} \end{align*}\]

For this process, the change in entropy of the universe is negative. Therefore, this process is not spontaneous.

Example – Entropy change for a phase transition – boiling water

Consider the following process:

\[\mathrm{H_2O}(l) \longrightarrow \mathrm{H_2O}(g)\]

We can use standard thermodynamic reference values (Thermodynamic Values Table) to estimate the entropy change for this process.

The selected values for this process is found to be

The change in entropy for this process/reaction (ΔS_rxn) is found by taking the entropies of the products and subtracting the entropies of the reactants.

\[\Delta S_{\mathrm{rxn}} = \sum_{\mathrm{products}} \left ( \nu \times S^{\circ} \right ) - \sum_{\mathrm{reactants}} \left ( \nu \times S^{\circ} \right )\]

We should be able to tell that the entropy change for this reaction is positive because:

1. This process is endothermic (absorbs heat)
2. This process increases the moles of gas in existence (gases have more entropy than solids or liquids)

Find the entropy change.

\[\begin{align*} \Delta S_{\mathrm{rxn}} &= \sum_{\mathrm{products}} \left ( \nu \times S^{\circ} \right ) - \sum_{\mathrm{reactants}} \left ( \nu \times S^{\circ} \right ) \\[1.5ex] &= \left [ \left ( 1 \times S^{\circ}_{\mathrm{H_2O}(g)} \right ) \right ] - \left [ \left ( 1 \times S^{\circ}_{\mathrm{H_2O}(l)}\right )\right ] \\[1.5ex] &= \left [ \left ( 1 \times 188.8~\mathrm{J~mol^{-1}~K^{-1}} \right ) \right ] - \left [ \left ( 1 \times 70~\mathrm{J~mol^{-1}~K^{-1}} \right )\right ]\\[1.5ex] &= 118.8~\mathrm{J~mol^{-1}~K^{-1}} \end{align*}\]

We can also find the enthalpy of reaction (ΔH_rxn) by performing a similar calculation using

\[\Delta H_{\mathrm{rxn}} = \sum_{\mathrm{products}} \left ( \nu \times \Delta H^{\circ} \right ) - \sum_{\mathrm{reactants}} \left ( \nu \times \Delta H^{\circ} \right )\]

Use the appropriate enthalpies from the table.

\[\begin{align*} \Delta H_{\mathrm{rxn}} &= \sum_{\mathrm{products}} \left ( \nu \times \Delta H^{\circ} \right ) - \sum_{\mathrm{reactants}} \left ( \nu \times \Delta H^{\circ} \right ) \\[1.5ex] &= \left [ \left ( 1 \times \Delta H^{\circ}_{\mathrm{H_2O}(g)} \right ) \right ] - \left [ \left ( 1 \times \Delta H^{\circ}_{\mathrm{H_2O}(l)}\right )\right ] \\[1.5ex] &= \left [ \left ( 1 \times -285.83~\mathrm{J~mol^{-1}~K^{-1}} \right ) \right ] - \left [ \left ( 1 \times -241.82~\mathrm{J~mol^{-1}~K^{-1}} \right )\right ]\\[1.5ex] &= 44.01~\mathrm{J~mol^{-1}~K^{-1}} \end{align*}\]

Notice that the enthalpy of reaction is the heat of vaporization (ΔH_vap) for water when using reference values scaled to 25 °C. This reaction is endothermic shown by the positive ΔH value.

Spontaneity using ΔS_universe

Use the entropy of the universe equation to determine the spontaneity of this process at two different temperatures of the surroundings.

Surroundings at 90 °C

\[\begin{align*} \Delta S_{\mathrm{universe}} &= \Delta S_{\mathrm{surroundings}} + \Delta S_{\mathrm{system}} \\[1.5ex] &= \dfrac{-44.01~\mathrm{kJ~mol^{-1}}}{363.15~\mathrm{K}}\left ( \dfrac{10^3~\mathrm{J}}{\mathrm{kJ}} \right ) + 118.8~\mathrm{J~mol^{-1}~K^{-1}} \\[1.5ex] &= -2.39~\mathrm{J~K^{-1}} \end{align*}\]

This process would not spontaneously occur at 90 °C as shown by the negative value for ΔS_universe.

Surroundings at 110 °C

\[\begin{align*} \Delta S_{\mathrm{universe}} &= \Delta S_{\mathrm{surroundings}} + \Delta S_{\mathrm{system}} \\[1.5ex] &= \dfrac{-44.01~\mathrm{kJ~mol^{-1}}}{383.15~\mathrm{K}}\left ( \dfrac{10^3~\mathrm{J}}{\mathrm{kJ}} \right ) + 118.8~\mathrm{J~mol^{-1}~K^{-1}} \\[1.5ex] &= 3.94~\mathrm{J~K^{-1}} \end{align*}\]

This process would not spontaneously occur at 110 °C as shown by the positive value for ΔS_universe.

Spontaniety using Gibbs free energy equation

We can use another equation (Gibbs free energy equation) to determine the spontaneity of a process.

\[\Delta G = \Delta H - T\Delta S\] We read this as the Gibbs free energy change of the system/reaction/process which is the difference between the enthalpy change and entropy change for the system/reaction/process at some temperature, T.

Any process is spontaneous if ΔG < 0 for that process. The enthalpy change (ΔH) for the boiling of water is 44.01 kJ mol^–1. The entropy change (ΔS) was determined above to be 118.8 J mol^–1 K^–1.

Find the free energy of reaction (ΔG) at the two different temperatures.

Surroundings at 90 °C

\[\begin{align*} \Delta G &= \Delta H - T\Delta S \\[1.5ex] &= \left (44.01~\mathrm{kJ~mol^{-1}} \right ) - \left [ \left (363.15~\mathrm{K} \right ) \left ( 118.8~\mathrm{J~mol^{-1}~K^{-1}} \right ) \left ( \dfrac{\mathrm{kJ}}{10^3~\mathrm{J}} \right ) \right ] \\[1.5ex] &= 0.88~\mathrm{kJ~mol^{-1}} \end{align*}\]

This process is not spontaneous at 90 °C as shown by the positive value for ΔG.

Surroundings at 110 °C

\[\begin{align*} \Delta G &= \Delta H - T\Delta S \\[1.5ex] &= \left (44.01~\mathrm{kJ~mol^{-1}} \right ) - \left [ \left (383.15~\mathrm{K} \right ) \left ( 118.8~\mathrm{J~mol^{-1}~K^{-1}} \right ) \left ( \dfrac{\mathrm{kJ}}{10^3~\mathrm{J}} \right ) \right ] \\[1.5ex] &= -1.51~\mathrm{kJ~mol^{-1}} \end{align*}\]

This process is spontaneous at 110 °C as shown by the negative value for ΔG.

Summary

Any spontaneous process has:

• ΔS_universe > 0
• ΔG < 0