# HF/STO-3G opt freqFirst Gaussian Job
Gaussian 09 is the quantum software package that you will use for your project. You will need two files:
The input file is the file that contains all the information about the computation you want to perform. It instructs the program (Gaussian 09) what level of theory you wish to invoke, what type(s) of job you want to perform, as well as the geometry of the chemical system you wish to analyze.
The PBS file contains the instructions that the supercomputer needs to serve your file to a node on the cluster.
Both the input file and the PBS file must be in the same directory.
Some helpful links:
This is a tutorial on fully characterizing the water molecule. All computed data corresponds to a single water molecule. You may hear this as “a water molecule in the gas phase” or “an isolated water molecule”. This tutorial assumes you are running Gaussian 09 on sequoia at MCSR.
The Input File
Route line
The route line begins with a ‘#’ symbol followed by a space. HF (i.e. Hartree-Fock) is the method. A forward slash ‘/’ separates the method and the basis set. ‘STO-3G’ is the basis set. ‘opt’ is the optimization keyword that tells Gaussian 09 to perform a geometry optimization. ‘freq’ tells Gaussian 09 to perform a harmonic vibrational frequency computation. A blank line follows the route section.
Comment line
water molecule optimization and frequency computationThe comment line is a line that can be anything. Usually a descriptive comment regarding the input file is placed here. A blank line follows the comment section.
Charge and Multiplicity
0,1The charge of the system is given followed by the multiplicity of the system. Here, the charge is 0 and the molecule is a singlet (multiplicity of 1).
Molecule Specification
Following the charge and multiplicity is the molecule specification. This example input file gives the water molecule in Cartesian coordinates (where the X, Y, and Z coordinates of each atom are given). The molecule specification is terminated with a blank line.
A visualization program (such as AGUI or Chemcraft) can take these coordinates and draw the molecule.
Submitting the Job
Once you have the input and PBS files ready, type the following on your command line and press enter.
$ qsub g09.pbsYou will notice an ID appear. Below is what appeared on my screen. This is the unique job ID for the job that was submitted to the cluster.
132001.sequoiaWhen the job starts, you will notice a new file 1.out appear in the local directory when typing ls. The program is writing the results of your computation to this output file.
The Output File
The output file (1.out) contains a lot of information that was generated from the computation that was performed. The information you will need from the output file will depend on what you are trying to do. Since we are performing an optimization and vibrational frequency computation, we will at the very least want the following data:
- Optimized geometry coordinates
- Electronic energy of the optimized geometry
- Number of imaginary vibrational modes
The output file is split into two main sections:
- Output from the geometry optimization
- Output from the frequency computation
Geometry Optimization
Head Matter
Lines 1-74 gets printed at the top of every output file you generate. It contains information about the program, the company, and citation data.
Program Version
Lines 75-78 show the program version that was used for the computation and the date it was run . Here, Gaussian 09 revision D01 was used. This is important to track when reporting computational results in a scientific paper. Notice how revision D01 was released on April 24, 2013.
******************************************
Gaussian 09: ES64L-G09RevD.01 24-Apr-2013
29-Jan-2019
******************************************Route Line
Lines 79-81 show the route line that was given in the input file.
--------------------
# HF/STO-3G opt freq
--------------------Internal Options
Lines 82-100 list the IOps (internal options) that the program is implementing for the computation. A complete set if IOps can be found on the IOps Reference page.
1/18=20,19=15,38=1/1,3;
2/9=110,12=2,17=6,18=5,40=1/2;
3/6=3,11=9,16=1,25=1,30=1,71=1/1,2,3;
4//1;
5/5=2,38=5/2;
6/7=2,8=2,9=2,10=2,28=1/1;
7//1,2,3,16;
1/18=20,19=15/3(2);
2/9=110/2;
99//99;
2/9=110/2;
3/6=3,11=9,16=1,25=1,30=1,71=1/1,2,3;
4/5=5,16=3,69=1/1;
5/5=2,38=5/2;
7//1,2,3,16;
1/18=20,19=15/3(-5);
2/9=110/2;
6/7=2,8=2,9=2,10=2,19=2,28=1/1;
99/9=1/99;Take a look at the first IOp.
1/18=20Here, IOp(1/18) is set to 20. Going to the IOps Reference page, look for Overlay 1 and find IOp(1/18). A value of 20 indicates that a full optimization will be performed in redundant internal coordinates (the default setting for an optimization). This means the Cartesian coordinate input will be translated into internal coordinates for the purpose of the optimization.
You can look up the over IOps if you wish.
Comment and Molecule Specification
Lines 101-108 show the comment line, charge/multiplicity, and molecule specification that was provided in the input file.
-----------------------------------------------------
water molecule optimization and frequency computation
-----------------------------------------------------
Symbolic Z-matrix:
Charge = 0 Multiplicity = 1
O 0. 0. 0.
H 0. 0. 1.
H 0. 1. 0. Initial Parameters
Lines 114-123 show the internal coordinates of the molecule. Bond lengths are given in Angstroms while angles and dihedrals/torsions are given in degrees.
----------------------------
! Initial Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.0 estimate D2E/DX2 !
! R2 R(1,3) 1.0 estimate D2E/DX2 !
! A1 A(2,1,3) 90.0 estimate D2E/DX2 !
--------------------------------------------------------------------------------Here, R1 is a length with a value of 1.0 Angstrom. It defines the distance between atoms 1 and 2 (i.e. R(1,2)). Atom 1 is an oxygen atom while atom 2 is the first hydrogen atom. R2 defines the distance between atoms 1 and 3 (oxygen and the second hydrogen atom). A1 is the angle between those atoms and is initially 90.0 degrees. We know from experiment that the bond angle in water is somewhere around 104.5 degrees. When the molecule is optimized, we should see this angle be closer to 104.5.
Stoichiometry
Line 142 gives the stoichiometry of the system.
Stoichiometry H2OFramework group
Line 143 gives the point group of the system.
Framework group C2V[C2(O),SGV(H2)]Gaussian recognized the molecule to be in C2v symmetry at this step. Sometimes as an optimization continues, symmetry may be lowered by the program.
NBasis and NBsUse
Lines 175-176 indicate the number of basis functions the computation has available (NBasis).
NBasis= 7 RedAO= T EigKep= 5.17D-01 NBF= 4 0 1 2
NBsUse= 7 1.00D-06 EigRej= -1.00D+00 NBFU= 4 0 1 2Here that number is 7. The STO-3G basis set gives 7 basis functions for the water molecule.
- 1 basis function per hydrogen atom (1s orbital)
- 5 basis functions for oxygen (1s, 2s, 2px, 2py, and 2pz orbitals)
Directly below, NBsUse is the number of basis functions that the computation is actually using. It is very important to make sure that the computation has used all the basis functions provided to it. In some cases, the program may throw away basis functions due to large overlaps. This is important to track and report when dealing with very high-level computations.
Orbital Symmetries
Lines 186-188 gives the occupied and virtual orbital symmetries.
Initial guess orbital symmetries:
Occupied (A1) (A1) (B2) (A1) (B1)
Virtual (A1) (B2)There are five molecular orbitals with A1, A1, B2, A1, and B1 symmetries. These are listed in increasing energy order (left to right).
SCF Done
Line 195 is the first time we have encountered the “SCF Done” line.
SCF Done: E(RHF) = -74.9611711632 A.U. after 7 cyclesThe self-consistent field (SCF) equations have been solved and the program is ready to move into the next step of the optimization. Atoms will be moved based on the forces they experience and the energy of the system will attempt to be lowered.
Convergence Block
Lines 290-294 prints the convergence thresholds and current values at the completion of an optimization step.
Item Value Threshold Converged?
Maximum Force 0.035640 0.000450 NO
RMS Force 0.022331 0.000300 NO
Maximum Displacement 0.077730 0.001800 NO
RMS Displacement 0.077731 0.001200 NO For the optimization to complete, some or all of the criteria must be met. Clearly none have been met as all the values are larger than the given thresholds and the word “NO” is printed for each.
Optimization Routine
Lines 418 to 768 shows more output information as the optimization continues. You can easily find more convergence blocks. Notice how the values begin to approach or fall below the thresholds. I also provide the SCF energy (in Hartrees) at each optimization step. Notice how the energy decreases throughout the computation.
Initial SCF energy:
SCF Done: E(RHF) = -74.9611711632 Optimization Step 1: Lines 413-417
SCF Done: E(RHF) = -74.9635236557 Item Value Threshold Converged?
Maximum Force 0.035640 0.000450 NO
RMS Force 0.022331 0.000300 NO
Maximum Displacement 0.077730 0.001800 NO
RMS Displacement 0.077731 0.001200 NO Optimization Step 2: Lines 535-539
SCF Done: E(RHF) = -74.9658964019 Item Value Threshold Converged?
Maximum Force 0.001729 0.000450 NO
RMS Force 0.001412 0.000300 NO
Maximum Displacement 0.002138 0.001800 NO
RMS Displacement 0.002174 0.001200 NO Optimization Step 3: Lines 648-652
SCF Done: E(RHF) = -74.9659009171 Item Value Threshold Converged?
Maximum Force 0.000405 0.000450 YES
RMS Force 0.000335 0.000300 NO
Maximum Displacement 0.000382 0.001800 YES
RMS Displacement 0.000418 0.001200 YESOptimization Step 4: Lines 761-765
SCF Done: E(RHF) = -74.9659012170 Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000013 0.001800 YES
RMS Displacement 0.000013 0.001200 YESLines 767-768 indicate that the optimization is completed.
Optimization completed.
-- Stationary point found.Optimized Parameters
Lines 769-778 show the optimized bond lengths and bond angle for the water molecule as computed at the HF/STO-3G level of theory.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.9894 -DE/DX = 0.0 !
! R2 R(1,3) 0.9894 -DE/DX = 0.0 !
! A1 A(2,1,3) 100.0281 -DE/DX = 0.0 !
--------------------------------------------------------------------------------Compare these values with the initial values (Lines 114-123).
Optimization Visualized
Below is an animation of the optimization of water. The input geometry has bond lengths of 1.000 Angstroms and a bond angle of 90.00 degrees. The program moves the atoms to lower the energy of the system. The optimized geometry has bond lengths of 0.989 Angstroms and a bond angle of 100.03 degrees.
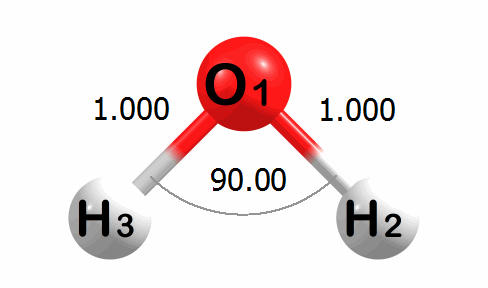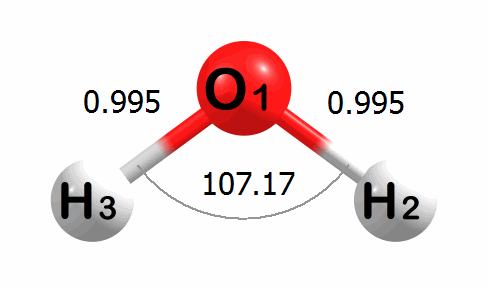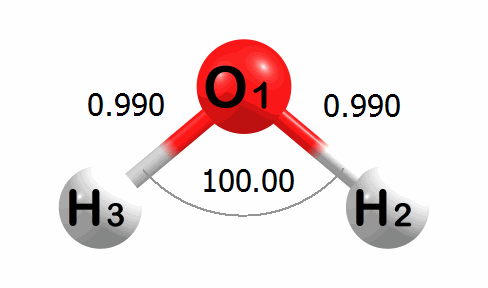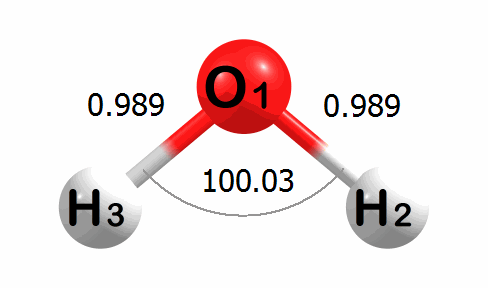
A corresponding plot of the energy change at each step of the optimization is given below. The energy change values are given in kcal mol-1.
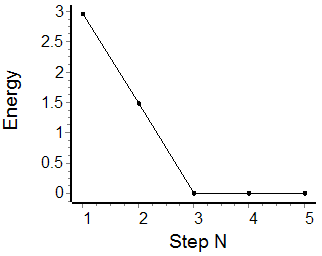
Notice how the energy is visually converged at steps 3-5.
Other Properties
Mulliken Charges
Lines 829-834 give the Mulliken charges for each of the atoms.
Mulliken charges:
1
1 O -0.330531
2 H 0.165266
3 H 0.165266
Sum of Mulliken charges = 0.00000Oxygen has a partial negative charge while the hydrogens have a partial positive charge. This is consistent with chemical intuition as oxygen is more electronegative than hydrogen.
Dipole moment
Lines 840-841 gives the dipole moment of the water molecule. Dipoles are directional so the magnitudes of the X, Y, and Z, vectors are printed.
Dipole moment (field-independent basis, Debye):
X=0.0000 Y=0.0000 Z=-1.7092 Tot=1.7092Here, the computed dipole moment of water is 1.71 D. A visualization program should be able to print this vector to the screen overlaid on the molecule.
The Archive
Lines 862-868 gives the archive to the job. An archive section is printed at the end of every successful job. The archive contains a summary of important information printed in a very condensed format.
1\1\GINC-N045\FOpt\RHF\STO-3G\H2O1\29-Jan-2019\0\\# HF/STO-3G op
t freq\\water molecule optimization and frequency computation\\0,1\O,0
.,0.0336169299,0.0336169299\H,0.,-0.0528571375,1.0192402076\H,0.,1.019
2402076,-0.0528571375\\Version=ES64L-G09RevD.01\State=1-A1\HF=-74.9659
012\RMSD=1.363e-12\RMSF=2.058e-06\Dipole=0.,0.4754949,0.4754949\Quadru
pole=-0.6028413,0.3014206,0.3014206,0.,0.,-0.3151241\PG=C02V [C2(O1),S
GV(H2)]\\@You should be able to spot the following information in the archive:
- Level of theory
- Date the job was run
- Stoichiometry of the molecule
- Comment
- Charge and multiplicity
- Cartesian coordinates of the optimized geometry
- Version of Gaussian
- Electronic state
- Hartree-Fock energy
- Dipole moment
- Point group (PG) of the molecule
Note that the final symmetry of the optimized molecule is still in C2v symmetry.
Electronic energy of optimized geometry
The absolute electronic energy of the optimized geometry will be critical to obtain. This can be found in a couple of places. One place is in the archive. The electronic energy is
HF=-74.9659012in Hartrees as computed at the HF/STO-3G level of theory. Be sure to catalog these in a spreadsheet for future data analysis when determining relative energies. Relative energies should be converted to more appropriate units such as kcal mol-1 or kJ mol-1 depending on the application. See Energy Conversion Values for conversion factors.
End Matter
Lines 871-876 prints the end matter of an output file. A normal termination of Gaussian results in the famous random quote as well as the relieving “Normal termination of Gaussian” line.
YOU CANNOT THROW TO THE GROUND THE LETTERS OF
THE GREEK ALPHABET AND PICK UP THE ILIAD.
- RUFUS CHOATE, 1799-1859
Job cpu time: 0 days 0 hours 0 minutes 5.2 seconds.
File lengths (MBytes): RWF= 5 Int= 0 D2E= 0 Chk= 1 Scr= 1
Normal termination of Gaussian 09 at Tue Jan 29 12:02:43 2019.Frequency Computation
The input file specified two jobs to be performed. We have just looked at the results of the optimization. Next is the corresponding frequency computation. Gaussian continues on to the second job and continues to print information to the same output file. Below is an excerpt of lines 878-903. Notice that Gaussian is reading in the optimized geometry from the optimization.
---------------------------------------------------------------
# N Geom=AllCheck Guess=TCheck SCRF=Check GenChk RHF/STO-3G Freq
---------------------------------------------------------------
Structure from the checkpoint file: "/tmp/132001.sequoia/Gau-28193.chk"
-----------------------------------------------------
water molecule optimization and frequency computation
-----------------------------------------------------
Charge = 0 Multiplicity = 1
Redundant internal coordinates found in file.
O,0,0.,0.0336169299,0.0336169299
H,0,0.,-0.0528571375,1.0192402076
H,0,0.,1.0192402076,-0.0528571375
Recover connectivity data from disk.The coordinate data was pulled from a temporary checkpoint file that was generated during the optimization routine. The same level of theory is used for the frequency computation.
Frequency Data
Lines 1097-1113 gives the vibrational frequency data along with other information (IR intensities, Raman activities, etc.). Units are defined.
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A1 A1 B2
Frequencies -- 2170.0323 4139.9917 4391.0683
Red. masses -- 1.0785 1.0491 1.0774
Frc consts -- 2.9923 10.5941 12.2392
IR Inten -- 7.2380 44.2856 29.9704
Raman Activ -- 9.2669 47.8207 21.5546
Depolar (P) -- 0.7246 0.1791 0.7500
Depolar (U) -- 0.8403 0.3038 0.8571
Atom AN X Y Z X Y Z X Y Z
1 8 0.00 0.00 0.07 0.00 0.00 0.05 0.00 0.07 0.00
2 1 0.00 -0.45 -0.54 0.00 0.57 -0.42 0.00 -0.54 0.45
3 1 0.00 0.45 -0.54 0.00 -0.57 -0.42 0.00 -0.54 -0.45Here, three harmonic vibrational frequencies were computed for the water molecule in A1, A1, and B2 symmetry. Notice that the frequencies are listed in increasing order. We can visualize these vibrations using visualization software.
Symmetric bend:
A1 symmetry – Frequency: 2170 cm-1
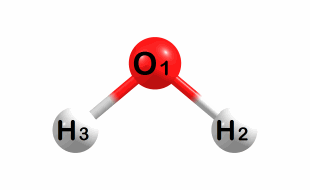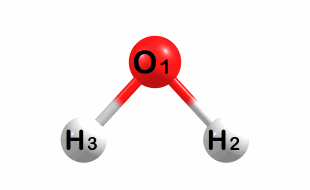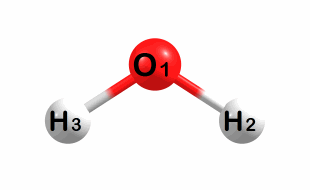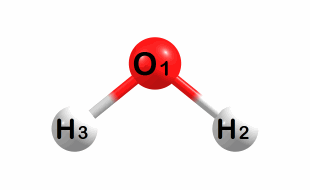
Symmetric stretch:
A1 symmetry – Frequency: 4140 cm-1
Anti-symmetric stretch:
B2 symmetry – Frequency: 4391 cm-1
Computed IR Spectrum:
A plot of the computed IR spectrum at the HF/STO-3G level of theory is given below.
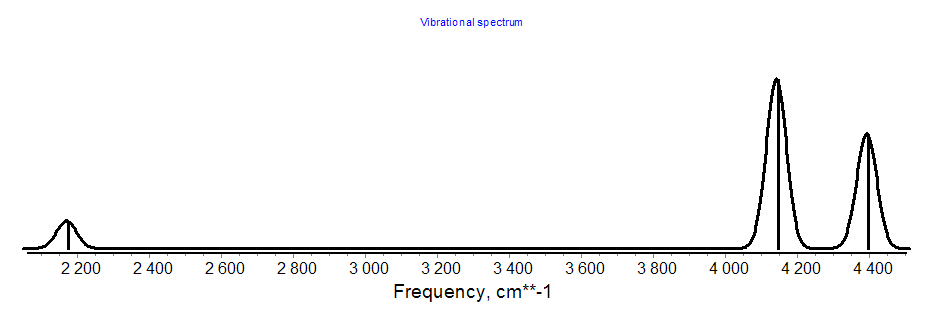
You should recognize that the plot was generated from the frequencies as well as the corresponding IR intensities for each mode.
Nature of the Stationary Point
The nature of the stationary point can be determined by looking at the computed vibrational frequencies. If all frequencies are real numbers, the optimized geometry is a minimum on the potential energy surface. If there is one imaginary mode of vibration (NOTE: Gaussian 09 reports imaginary modes a negative numbers), the structure is a transition-state. If more than one mode is imaginary, a higher-order saddle point was characterized. In general, minimum energy structures and transition states are relevant.
For our water molecule, all computed vibrational frequencies are positive, real numbers. Therefore, we have identified a minimum energy structure at the HF/STO-3G level of theory.
Thermochemistry Data
Frequency computations produce thermochemistry data (lines 1115-1161).
-------------------
- Thermochemistry -
-------------------
Temperature 298.150 Kelvin. Pressure 1.00000 Atm.
Atom 1 has atomic number 8 and mass 15.99491
Atom 2 has atomic number 1 and mass 1.00783
Atom 3 has atomic number 1 and mass 1.00783
Molecular mass: 18.01056 amu.
Principal axes and moments of inertia in atomic units:
1 2 3
Eigenvalues -- 2.58405 4.13667 6.72072
X 0.00000 0.00000 1.00000
Y 1.00000 0.00000 0.00000
Z 0.00000 1.00000 0.00000
This molecule is an asymmetric top.
Rotational symmetry number 2.
Rotational temperatures (Kelvin) 33.51862 20.93803 12.88757
Rotational constants (GHZ): 698.41559 436.27830 268.53371
Zero-point vibrational energy 64006.7 (Joules/Mol)
15.29798 (Kcal/Mol)
Vibrational temperatures: 3122.19 5956.52 6317.76
(Kelvin)
Zero-point correction= 0.024379 (Hartree/Particle)
Thermal correction to Energy= 0.027212
Thermal correction to Enthalpy= 0.028156
Thermal correction to Gibbs Free Energy= 0.006641
Sum of electronic and zero-point Energies= -74.941522
Sum of electronic and thermal Energies= -74.938689
Sum of electronic and thermal Enthalpies= -74.937745
Sum of electronic and thermal Free Energies= -74.959260
E (Thermal) CV S
KCal/Mol Cal/Mol-Kelvin Cal/Mol-Kelvin
Total 17.076 5.968 45.282
Electronic 0.000 0.000 0.000
Translational 0.889 2.981 34.608
Rotational 0.889 2.981 10.673
Vibrational 15.298 0.006 0.001
Q Log10(Q) Ln(Q)
Total Bot 0.881609D-03 -3.054724 -7.033762
Total V=0 0.144132D+09 8.158759 18.786237
Vib (Bot) 0.611687D-11 -11.213471 -25.819971
Vib (V=0) 0.100003D+01 0.000012 0.000028
Electronic 0.100000D+01 0.000000 0.000000
Translational 0.300432D+07 6.477746 14.915562
Rotational 0.479734D+02 1.681001 3.870647Energies for zero-point, enthalpy, and free energy corrections to the electronic energy are given in Hartrees.
A detailed description of this data can be found here.
Comparisons to other levels of theory
We have just run our HF/STO-3G computation on the water molecule. Run another job at the MP2/aug-cc-pVDZ, MP2/aug-cc-pVTZ, and MP2/aug-cc-pVQZ levels of theory (cc basis sets denoted as aDZ, aTZ, and aQZ, respectively) and compare the job run times, geometrical parameters, and vibrational frequencies.
MP2 is a more rigorous method than HF. Furthermore, aTZ is a larger basis set than aDZ and STO-3G. We would expect better results from the higher level of theory and the larger basis set.
Below are some tabulated data from these three computations compared to experimental data.
Which level of theory most agreed with experiment? Which one did not? Which job took the longest? Which one was the fastest?